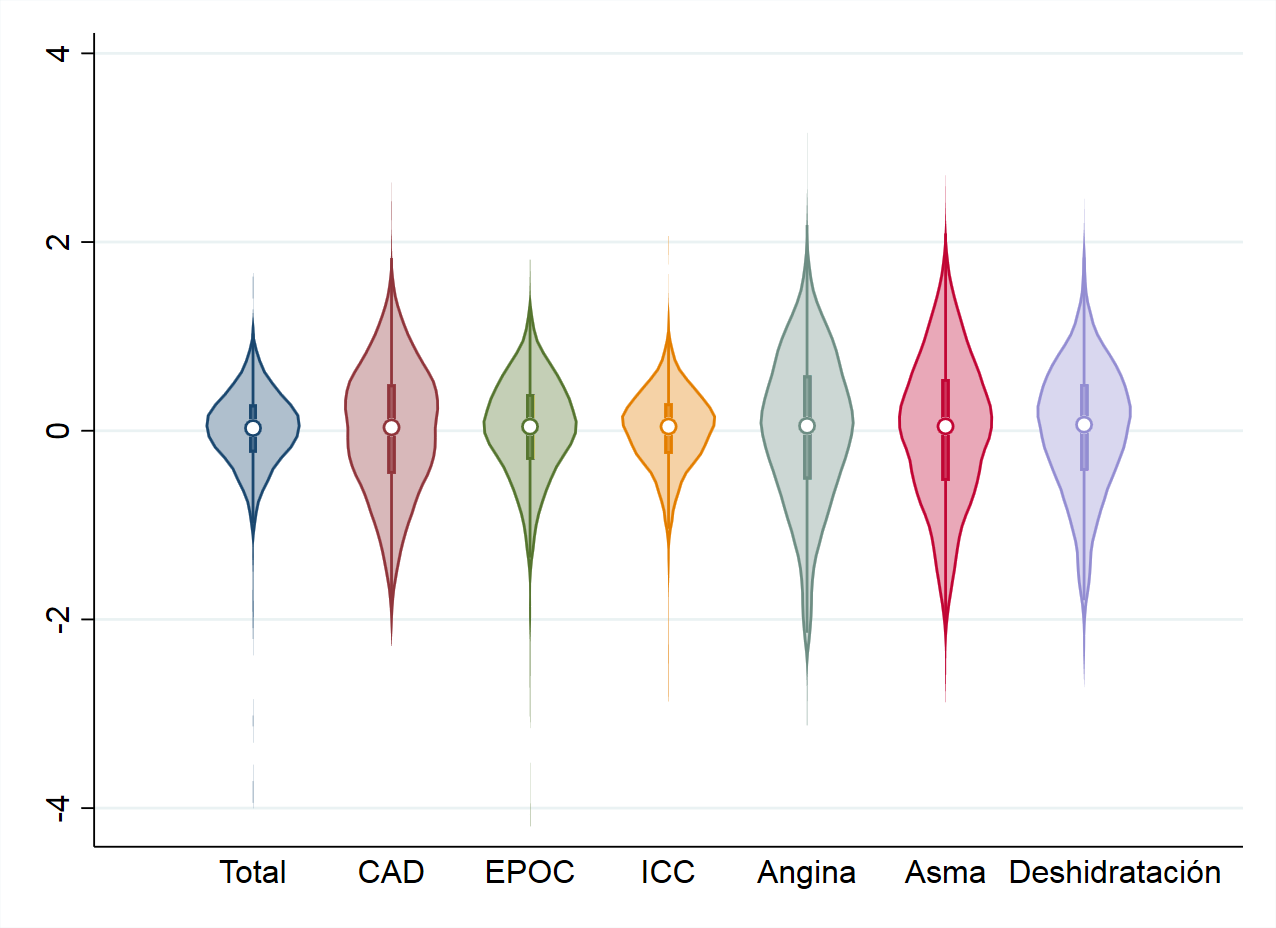
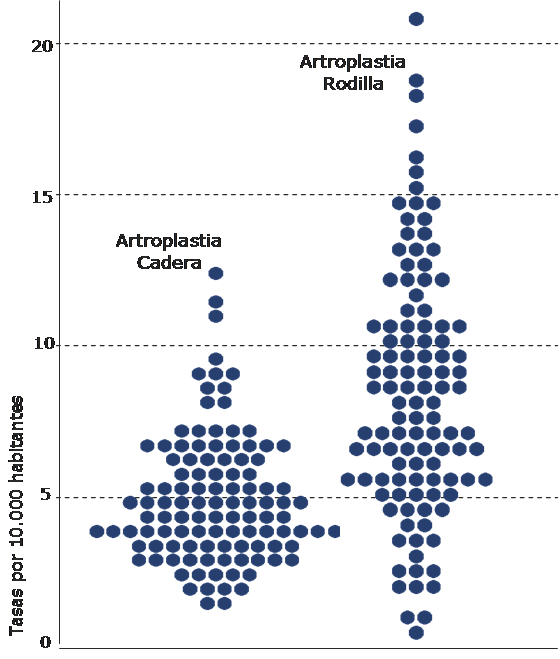
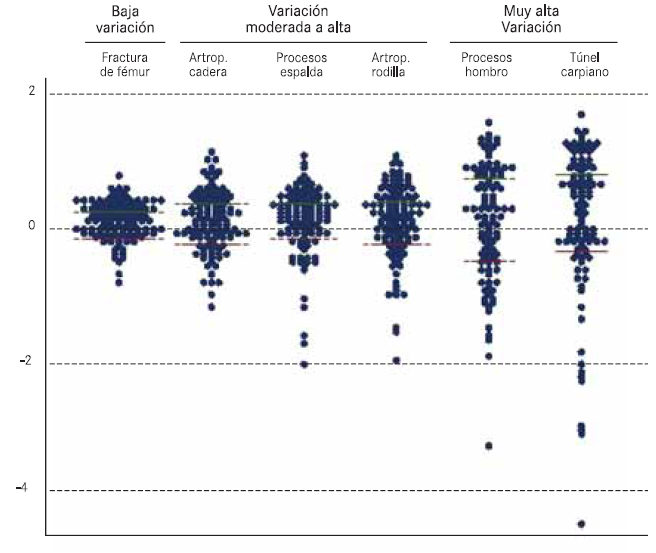
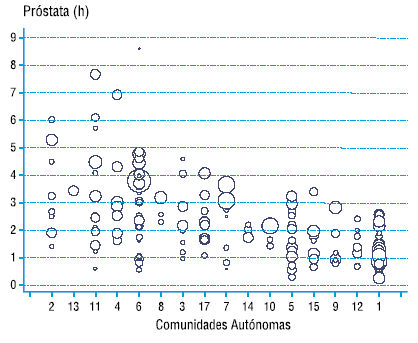
– Variation ratio
The variation ratio (RV) is the quotient between the highest and the lowest value of the standardised rates for all the basic areas and/or zones studied.
It is widely used due to its simplicity and highly intuitive nature. However, it has important limitations, since it is very sensitive to low rates, differences in population size between areas, re-entries and extreme values. It is statistically weak and, if any area has no events -usually in studies in small areas- it offers incongruent values. Currently, it is commonly replaced by the variation ratio between areas at the 95th and 5th percentiles (RV95-5) which reduces the effect of extreme values, and accompanied by the variation ration between the 75th and 25th percentiles (RV75-25) which gives an idea of the variability in the main 50% of observations.
– Unweighted Coefficient of Variation, CVu or CV
This is the quotient of the standard deviation and the mean. The CV expresses the value of the standard deviation in mean units with the advantage, compared to the standard deviation, of not depending on the units of measurement. It can be interpreted in terms of relative variation (more variability the higher the value of the coefficient).
– Weighted Coefficient of Variation, CVw
This is the quotient of the standard deviation between areas and the average between areas, weighted by the size of each area. The CVw is similar to the CVu, although it attaches greater weight to areas with a larger number of inhabitants and better supports the presence of areas with different population sizes. It is one of the statistics of choice when the size of the areas is very different.
– Systematic Component of Variation, SCV
This measures the variation of the deviation between the observed and expected rate, expressed as a percentage of the expected rate. It is a measure derived from a model that recognises two sources of variation: systematic variation (difference between areas) and random variation (difference within each area). This measures the variation of the deviation between the observed and expected rate, expressed as a percentage of the expected rate. The greater the SCV, the greater the systematic variation (not expected by chance).
– Empirical Bayes statistic, EB
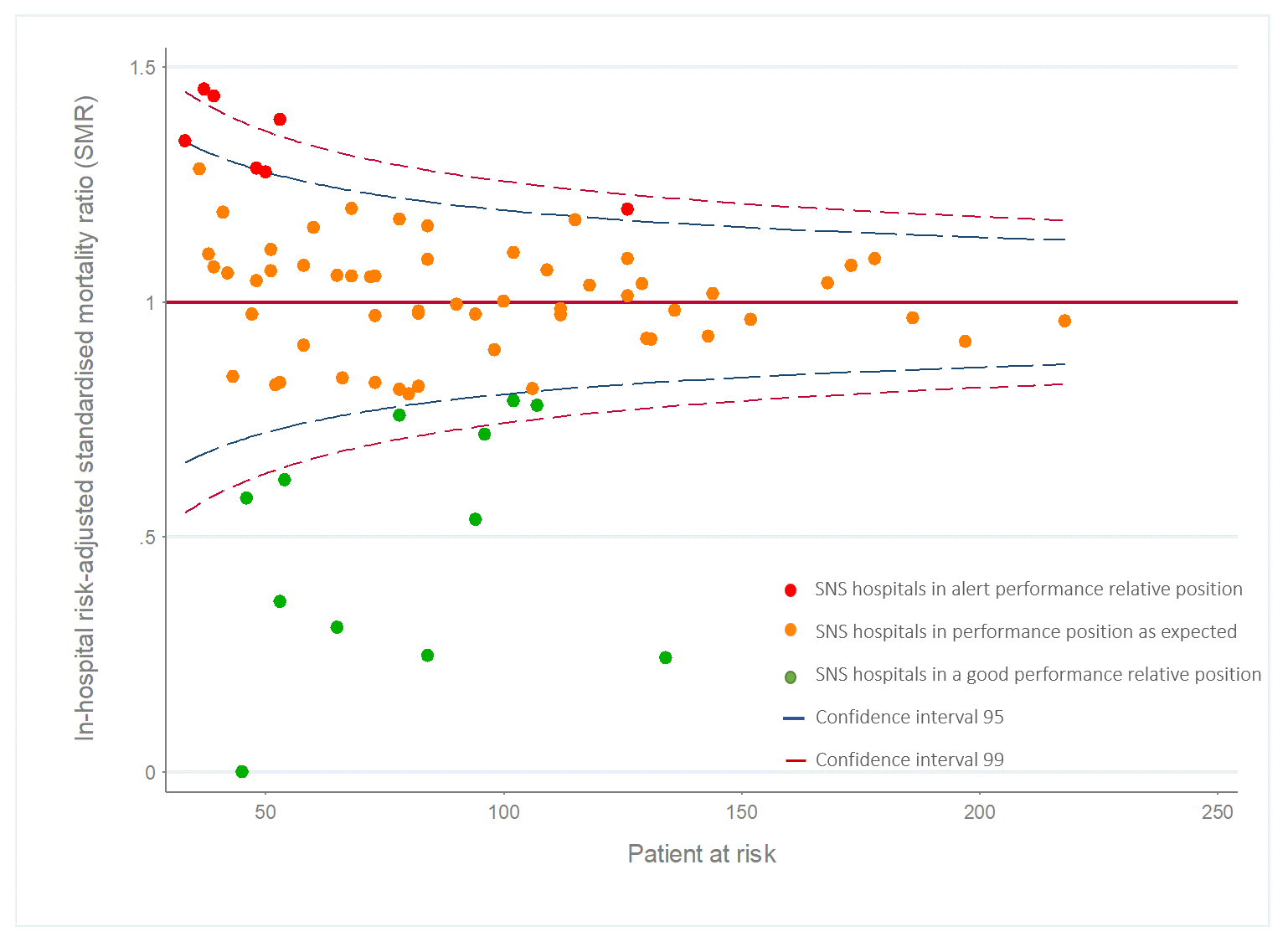
The SHR, is an estimator of the “relative risk” of each area, namely, the risk of use in relation to the group considered as the benchmark and depends largely on the population size (its variance is inversely proportional to the expected cases). In this respect, extreme SHRs, and therefore those dominant in the apparent geographical pattern, are the least accurate estimates from areas with few cases. On the other hand, the variability of observed cases is usually much higher than expected in a Poisson distribution (extra-variability).
In order to solve these problems, several alternatives have been proposed. Assuming that the observed cases are distributed in a Poisson distribution, the Bayesian empirical method also assumes that SHR is a random variable that, in our case, follows a log-normal distribution [log(ri) ~ N(m, s2)]. This model is known as a log-normal Poisson mixed model. The EB statistic used here is the estimate of the variance of the log-normal distribution that best fits (likelihood) the geographical pattern of the SHR, taking into consideration the precision of its estimates. It is obtained by the Penalized Quasi Likelihood method. Although it is not very intuitive (it must be interpreted in terms of relative variation), in empirical studies, the EB behaves as a powerful statistic in terms of detecting variability while being the most stable in terms of variability between areas and small frequencies.